Unveiling the Odd Marble
You’re given a balance scale and 12 marbles. Out of the 12, 11 are identical and there’s one marble that’s either heavier or lighter - we don’t know. The task is to identify this different marble and whether it’s lighter or heavier using the balance only 3 times.
Let’s now confirm whether it’s possible to achieve this. Each time we use the balance, we get one of three results: left side heavier (LHS > RHS), both sides equal (LHS = RHS), or right side heavier (LHS < RHS).
So if we use the balance 3 times, we can have 3x3x3=27 unique outcomes. We need to account for each marble possibly being the odd one out (lighter or heavier) or all marbles being equal. This means we have 2x12+1=25 unique scenarios to cover.
Since we have more potential balance outcomes (27) than we do marble scenarios (25), we theoretically have the potential to design the balance tests so each distinct outcome corresponds to a unique scenario. The structure of how these tests might look is suggested below:
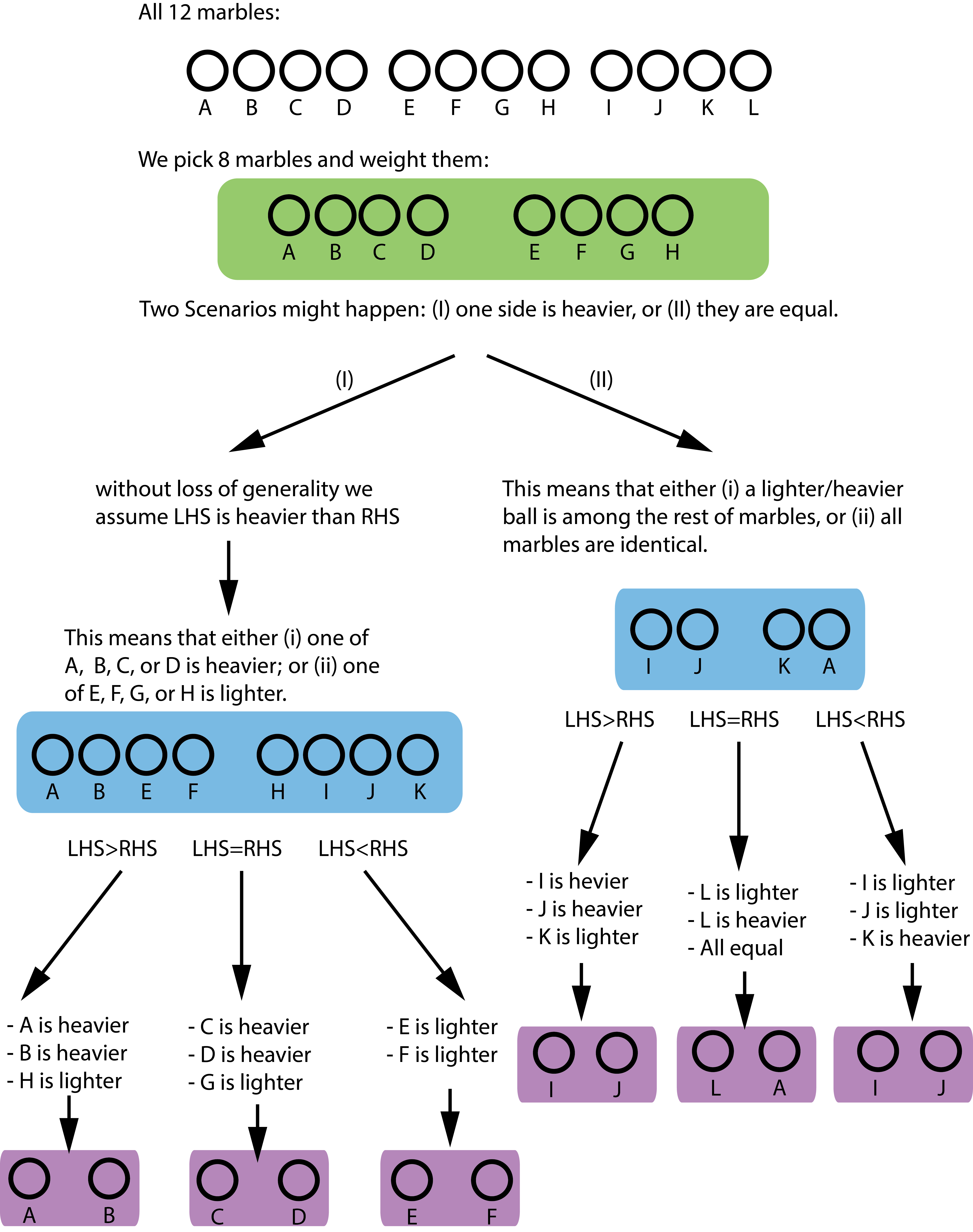
To generalize this question, if we have \( n \) marbles with one being lighter/heavier or maybe equal, we will have \( 2n+1\) cases, for which we need at least \(m \) where \( 3^m \geq 2n+2\).