Buffon's Needle
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle lie in one of the the two strips?
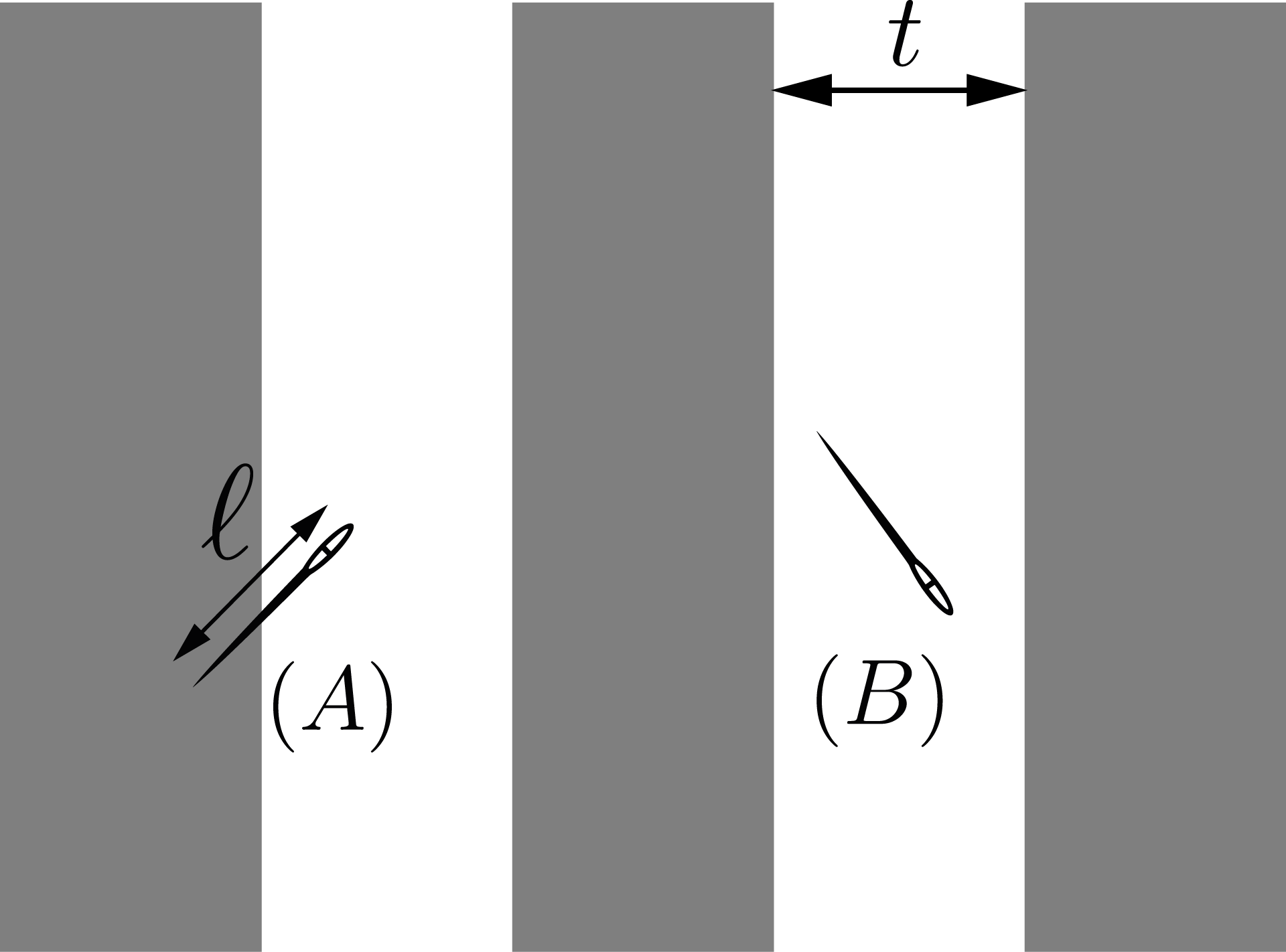
e.g. here in (A) the needle lies on the border line between the stripes and in (B) the needle lies in the white strip. The equation asks what is the probability of observing case (B)?
In order to find the probability, we need to look at the space of possible configuration for the needle and see how much of this configuration space is the part that we are interested in.
The center of needle has a distance \(x\) from the beginning of the strip and we assume an angle of the needle is
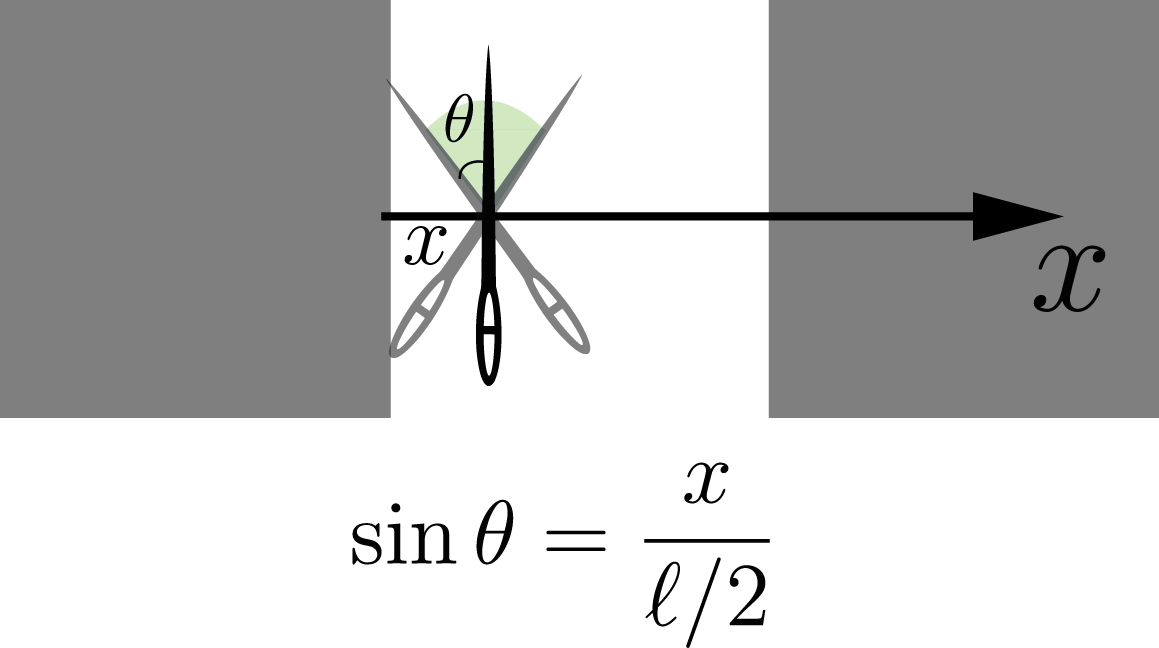
Looking at the area in the configuration space of \((x,\theta)\) we find that there will be two cases depending on if \(x\leq \ell\) or \(x\geq \ell\). You can see the different cases in the following figure. The full configuration space is the whoe ractangle with the area of $\pi\cdot t$; and what we are interested in is the green area.

So the total are is \(A = \pi t\)
The relevant area for which the needle lies in between the stripes is
\[A_g = \iint d\theta dx\]and the probability is simply \(p = A_g/A\)
No in order to calculate the $A_g$ we have
(a) \(t\geq \ell\):
In this case, we have
\[A_g = 4 \int_{0}^{\pi/2} d\theta~ \int_{\frac{\ell}{2}\sin\theta}^{t/2} dx = 2 \int_{0}^{\pi/2} {t} - {\ell} \sin\theta d\theta = {\pi t} - 2{\ell}\]As a result
\[p = \frac{\pi t - 2 \ell}{\pi t} = 1 - \frac{2\ell}{\pi t}\](b) \(t\leq \ell\):
We can take the integral as follows
\[A_g = 4\int_0^{\sin^{-1}(t/\ell)} d\theta \int_{\ell \sin\theta/2}^{t/2} dx = 2\int_0^{\sin^{-1}(t/\ell)} (t - \ell \sin\theta )d\theta \\\] \[A_g = 2t\sin^{-1} \frac{t}{\ell} - 2 \ell \left[ \cos(\sin^{-1}\frac{t}{\ell}) - 1\right]\]So the probability becomes
\[p = \frac{2}{\pi} \sin^{-1}\frac{t}{\ell} - \frac{2\ell}{\pi t} \left[ \cos(\sin^{-1}\frac{t}{\ell}) - 1 \right]\]So the probability of the needle lie in between the strips and not cross them is
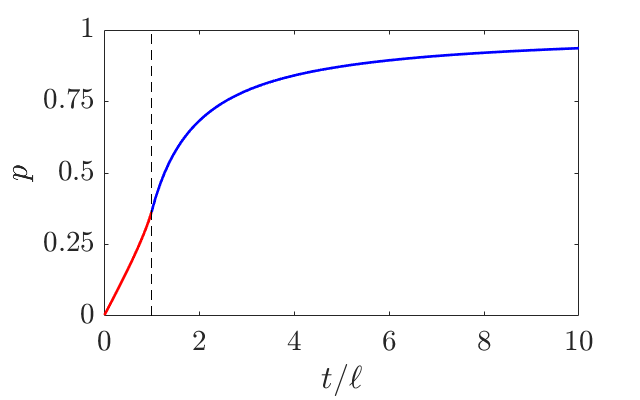
\[p = \begin{cases} \frac{2}{\pi} \sin^{-1}\frac{t}{\ell} - \frac{2\ell}{\pi t} \left[ \cos(\sin^{-1}\frac{t}{\ell}) - 1 \right] & t\leq \ell \\ 1 - \frac{2\ell}{\pi t} & t\geq \ell \end{cases}\]and finally this is what the probability looks like!