Maximizing Consumption from Investment
Today, I was pondering on the subject of investment. Specifically, I was wondering what to do if I invested an initial amount of money (let’s call it \(X_0\)) for a certain period (let’s say \(T\) years) with an expected return rate of \(r\%\). The question I had was whether I should spend the interest earned or reinvest it back into my account given the following assumption: I would like to maximize my consumption from this investment. Here’s the formal question in a simplified way:
Imagine you’re an investor who’s put in a certain amount of money \(X_0\) into an investment at time zero \(t=0\). This money is locked in for investment purposes and cannot be withdrawn. This investment yields an annual interest of \(r\%\) for a total duration of $T$ years. Each year, you have the option to spend a portion \(a(t)\) of the interest earned and reinvest the remaining amount \(1 - a(t)\). The challenge is to figure out what fraction of the yearly interest should you spend in order to maximize the total consumption (money withdrawn for expenses) over the investment period.
In order to solve this, first I assume that the time is continuous (that’s how I roll!). So, our money follows the following ODE
\[\frac{dX}{dt} = r X(t) (1-a(t))\]where \(r\) is the continuous interest rate. At the same time, the amount of money consumed is the following
\[C = \int_0^T r X(t) a(t) dt\]So our question, in mathematical terms is to find the best consumption plan \(a^*(t)\) such that our consumption is maximized, in other words
\[a^*(t) = \text{arg} \max_{a(t)} \int_0^T r X(t) a(t) dt \label{eq:1}\\ \text{such that } \frac{dX}{dt} = r X(t) (1-a(t))\]Note that \(0 \leq a(t) \leq 1\). The dynamics equation (second equation) has an easy answer
\[X(t) = X_0 \exp\left( {rt - r\int_0^t a(t) dt}\right)\]Now inserting this result into the first equation, we find the consumption as
\[a^*(t) = \text{arg} \max_{a(t)} r\int_0^T r X(t) a(t) dt = \text{arg} \max_{a(t)} \int_0^T r ~ X_0 ~ a(t) \exp\left( {rt - r\int_0^t a(t) dt}\right) dt\]and our goal is to find a function \(a(t)\) that maximizes the above integral, which is our consumption. This ridiculously looks like Euler-Lagrange equation. Let’s define \(b'(t) \equiv a(t)\) or equivalently \(b(t) = \int_0^t a(t') dt'\). Then our optimization problem becomes
\[b^*(t) = \text{arg} \max_{b(t)} \int_0^T r ~ X_0 ~b'(t) \exp\left( {rt - rb(t)} \right) dt\]Now it’s actually the same as Euler-Lagrange equation, where the Lagrangian is \(L(t,b(t),b'(t)) = r ~ X_0 ~b'(t) \exp\left( {rt - rb(t)}\right)\). So we use the Euler–Lagrange equation
\[\frac{\partial L}{\partial b(t) } = \frac{d}{dt} \frac{\partial L}{\partial b'(t)} \\ -r b'(t) = r-rb'(t)\]Alright, so it seems that there is no solution here. This actually means that the extremums happen at the boundaries. Since \(0 \leq a(t) \leq 1\), then it means that it happens when \(a = 0, \text{ or } 1\). Physically speaking, it means that when we are either completely re-investing or completely consuming the interest payments. Alright, saving all the time is not the maximum, because it results in no consumption or \(C=0\). Spending all the interest we earn or \(a(t) = 1\) can be a solution. This basically means that our money is not growing in the fund, and it remains constant at \(X_0\), and we are always consuming the interest payments. This can also be seen in the equations, since
\[C = \int_0^T r ~ X_0 dt = r X_0 T\]Now we need to be careful. There are other boundary solutions that we can construct as well. Imagine the following plan: assume we re-invest the interests we earn for \(0 \leq t \leq T_c\) and then start spending all the interest at \(t\geq T_c\). This plan is again some boundary solution and could be an extremum. We need to calculate the consumption. So the plan is the following
\[a(t) = \begin{cases} 0 & 0 \leq t \leq T_c\\ 1 & T_c \leq t \leq T \end{cases}\]Let’s see how much consumption we can get from this plan.
\[C = \int_{T_c}^T r ~ X_0 ~ \exp\left( rt - r(t-T_c) \right) dt = \int_{T_c}^T r ~ X_0 ~ \exp\left( r T_c \right) dt = r X_0 (T-T_c) \exp \left( r T_c \right)\]In order to find the maximum of the above consumption, we take the derivative with respect to \(T_c\) to find
\[-1 + (T-T_c) r = 0 \quad \to \quad T_c = T - \frac{1}{r}\]Not that in order for \(T_c \geq 0\), then \(rT \geq 1\). For such \(T_c\), we find
\[C = X_0 \exp\left( rT - 1\right)\]Let’s plot the different solutions consumption
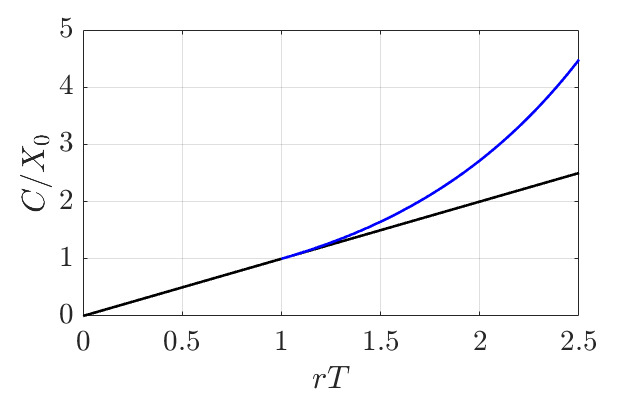
So basically, upto \(rT=1\), it makes sense to consume all the interest payments, and for \(rT\geq1\) it’s better to wait until \(T_c = T-\frac{1}{r}\) and then consume all the interest payments. To give it a more physical sense, assume you have a fund with \(10\%\) APR, this means that \(\exp(r)-1 = 0.1\) or \(r= \log(1.1) \approx 0.04\). Now, if your goal is to invest for less than 25 years \((25\times 0.04 =1 )\), you better use all the interest payments you’re paid to maximize your consumption. If you are investing for more than 25 years, its better to re-invest all the interests for the first 25 years, and after that consume all the interest payments.