Option Pricing
Recently, I’ve developed a fascination for options trading and the mechanisms behind their pricing. This piece is aimed at sharing my understanding so far about options and their pricing structure. I’ll start with the basics of options, then move onto discussing the limits within which an option’s price can fluctuate. Subsequently, I’ll shed some light on concepts like the Weiner process and the Ito process. To round off, I’ll derive the well-known Black-Scholes equation. Please note: I don’t come from a financial background, so what I’m sharing here are my personal interpretations and learning.
Options
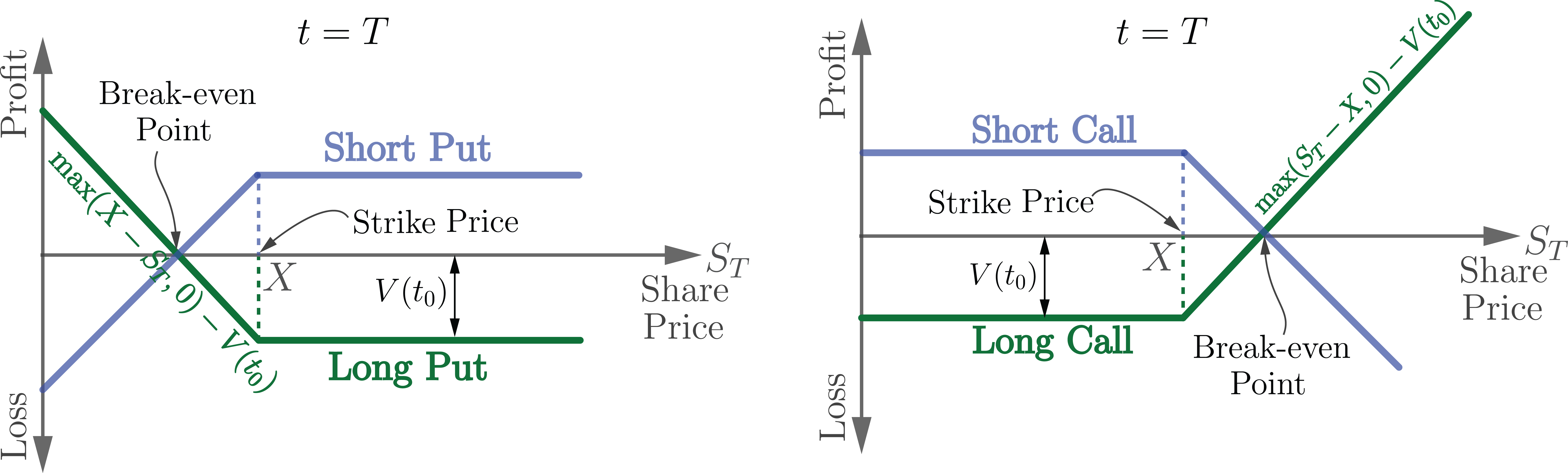
An options is a contract that gives the buyer the option, but not obligation, to buy (i.e., Call option) or sell (i.e., Put option) an asset (such as stock) at a specific strike price before a certain date (American option) or at a certain date (European option).
To make it easier we focus on European options. In summary we then have the following two primary option categories: calls and puts.
- Call: The right to purchase stock at the strike price \(P\) from the seller of the option at time \(T.\)
- Put: The right to sell a stock at price \(P\) to the seller of option at time \(T\).
The objective of option pricing is to answer how much an option contract worth at time \(t<T\) ?
Interest rate
Interest rate is the cost of borrowing money. If you borrow/lend \(X\)amount of money, you are expected to give-back/take \(Xe^{rT}\) after time \(T\). Basically it means time is money.
Bounds on Option Price
We can find bounds on the values of options.
Call Option:
The price of a call option \(c\) at the time of purchase \(t=t_0\) is \(c = \mathbb{E}(S_T) - X\). The price of an option cannot be larger than the stock price, i.e., \(\boxed{c \leq S_0}\). If this was the case, one would sell the call options, buy the stock and invest the rest. On the other hand to find the lower bound, consider the following portfolios
- One call option and \(Xe^{-rT}\) amount of money invested risk-free
- One stock at \(S_0\)
In the first scenario the bond worth \(X\) amount of money, and the call option worth \(\max(S_T-X,0)\), so in total we will have \(X+\max(S_T-X,0) = \max(S_T,X)\) The second portfolio however worth \(S_T\). comparing the two, we find that
\[\text{since } \max(S_T,X) \geq S_T \to c + Xe^{-rT} \geq S_0 \to \boxed{c \geq S_0 - Xe^{-rT}}\]Put Option
The value of a put option is \(p = X-\mathbb{E}(S_T)\). The put option can not worth more than the discounted value of the strike price, i.e., \(\boxed{p \leq Xe^{-rT}}\). Since if this wasn’t the case, one would sell the put option, invest the money, and at the exiration date, he will have more money that he needs for settlement. To find the lower bound, we consider the following portfolios
- One put option \(p\) and one stock \(S_0\)
- A bond paying \(X\) at time \(t=T\). It should basically cost \(Xe^{-rT}\).
In the first scenario, the stock worth \(S_T\), and the put worth \(\max(X-S_T,0)\). So the portfolio, worth \(\max(X,S_T)\). on the other hand, the second portfolio worth \(X\). As a result, we have
\[\text{since }\max(X,S_T) \geq X \to p + S_0 \geq Xe^{-rT} \to \boxed{p \geq Xe^{-rT}-S_0}\]Put-Call Parity
\[\text{call option at }c \text{ matures to } \max(S_T-X,0) \\ \text{put option at }p \text{ matures to } \max(X-S_T,0) \\\]No, imagine we buy a call option and a bond at \(Xe^{-rT}\) on one hand, and a put option and a stock at \(S_0\). The portiolios then become
- call option \(c\) + bond \(Xe^{-rT}\) matures to \(\max(S_T-X,0) + X = \max(S_T,X)\)
- put option \(p\) + stock \(S_0\) matures to \(\max(X-S_T,0) + S_T = \max(X,S_T)\)
Since these two profiles have the same maturity, they should be equal or
\[\boxed{c + Xe^{-rT} = p + S_0}\]The above equation is known as put-call parity which relates the price of a call option to the price of a call option.
Weiner Process
A variable \(z\) follows a Weiner process, if the following two properties hold
- The change \(\Delta z\) during period \(\Delta t\), is \(\Delta z = \epsilon \sqrt{\Delta t}\), where \(\epsilon\) has a standard normal distribution with mean zero and standard deviation unity, i.e., \(\epsilon \in \mathcal{N}(0,1)\).
- The values of \(\Delta z\) fr any two short intervals of time, \(\Delta t\), are independent.
From the first property, we can conclude that \(\Delta z\) has a normal distribution as \(\mathcal{N}(0,\Delta t)\). If we also consider the changes from \(t=0\), to \(t=T\), we have
\[z(T)-z(0) = \sum \epsilon_i \sqrt{\Delta t}\]where all of the \(\epsilon_i\)s are independent and are distributed \(\mathcal{N}(0,1)\). Since \(\epsilon_i\)s are independent, then \(z(T)-z(0) \in \mathcal(0,N\Delta t) = \mathcal{N}(0,T)\).
Generalized Weiner Process
A generalized Weiner process for a random variable \(x\) is defined as
\[\Delta x = a \Delta t + b \epsilon \sqrt{\Delta t}\]where \(a,b\) are constants. If \(a\) and \(b\) are a function of \(x,t\) then, this process is called an Ito Process.
Ito’s Lemma
Suppose a random variable \(x\) follows an Ito process
\[dx = a(x,t) dt + b(x,t) dz\]If \(G\) is a function of \(x\) and \(t\), then
\[dG = \left(\frac{\partial G}{\partial t} + \frac{\partial G}{\partial x} a + \frac{1}{2}\frac{\partial^2 G}{\partial x^2} b^2\right) dt + \frac{\partial G}{\partial x} b ~dz\]Stock Price as Random Walk
Stock price return does a random walk with drift \(\mu\) and
\[\frac{dS}{S} = \mu dt + \zeta\]where \(\zeta\) is a noise term (e.g., Gaussian) with standard deviation \(\zeta_0\) and vanishing mean. Each time step has a variance of \(\zeta_0^2\), and the number of steps are \(t/dt\). Therefore the standard deviation will be \(\zeta_0 \sqrt{t/dt}\). In order for the limit of \(dt\to0\) to make sense, \(\zeta_0 \propto \sqrt{dt}\). Therefore, we write the noise term as \(\zeta=\sigma \epsilon \sqrt{dt}\) , where \(\sigma\) is the volatility of the stock return and \(\epsilon\) is a Gaussian random number with zero mean and unit standard deviation \(\mathcal{N}(0,1)\).
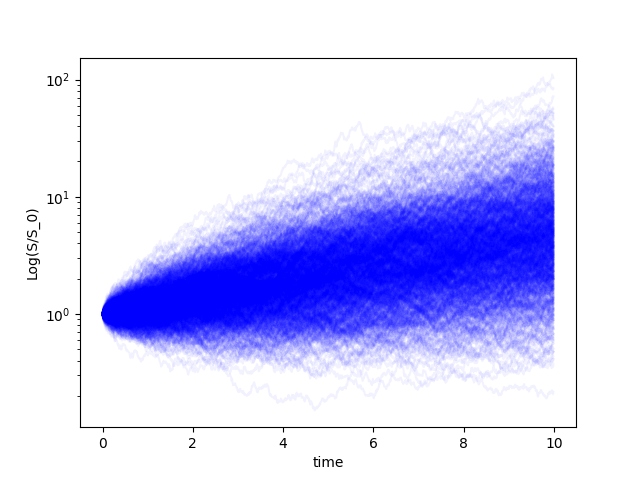
Let’s first take a look at the stocks random walk. In the following we assume a \(15\%\) return (\(\mu = 0.15\)) and a volatility of \(30\%\) (\(\sigma =0.15\)).
import numpy as np
import matplotlib.pyplot as plt
S0 = 1.; dt=0.01; mu=0.15; sigma=0.3; T = 10;
t = np.arange(0,T,dt)
for j in range(1000):
S = np.zeros(t.shape)
S[0] = S0;
for i in range(0,int((T-dt)/dt)):
S[i+1]=S[i]*np.exp(mu*dt+np.random.randn(1)[0]*sigma*np.sqrt(dt));
plt.plot(t,S,alpha=0.05,color='b')
plt.yscale('log')
plt.xlabel('time')
plt.ylabel('Log(S/S_0)')
plt.show()
In summary we had
\[dS = \mu S dt + \sigma S dz\]Now, imagine that \(G = \ln S\), from Ito’s Lemma, we have
\[\frac{\partial G}{\partial S} = \frac{1}{S}, \quad \frac{\partial^2 G}{\partial S^2} = \frac{-1}{S^2}, \quad \frac{\partial G}{\partial t} = 0\]As a result, we find that
\[dG = \left( \mu - \frac{\sigma^2}{2}\right) dt + \sigma dz\]So, we can say that
\[\ln S_T - \ln S_0 \sim \mathcal{N}\left( (\mu - \frac{\sigma^2}{2})T, \sigma^2 T\right)\]Example. Imagine a stock price of \(10\$\), with annual return of \(16\%\), and volatility of \(20\%\). After \(6\) months, what is the probability distribution of stock price?
\[\ln S_T - \ln10 \sim \mathcal{N}\left( (0.16-\frac{0.2^2}{2})\frac{1}{2}, 0.2^2 \frac{1}{2} \right)\\\] \[\ln S_T - \ln10 \sim \mathcal{N}\left(0.07, 0.2 \right)\\\] \[10 e^{0.07-0.2}\leq S_T \leq 10 e^{0.07+0.2} \to 8.78 \leq S_T \leq 13.10\]with \(90\%\) probability the stock price lies in this interval.
Derivation of Black-Scholes-Merton
Assume \(f\) is the price of an option at time \(t\) contingent of stock \(S\). The variable \(f\) should be a function of \(S\) and t. Using Ito’s lemma, we have
\[df = \left( \frac{\partial f}{\partial t} + \frac{\partial f}{\partial S} \mu S + \frac{1}{2} \frac{\partial^2 f}{\partial S^2} \sigma^2 S^2 \right) dt + \frac{\partial f}{\partial S} \sigma S dz\]Imagine a portfolio \(\Pi\) made of \(-1\) derivative and \(\partial f/\partial S\) shares, i.e.,
\[\Pi = -f + \frac{\partial f}{\partial S} S\]The change in the portfolio then becomes
\[\Delta \Pi = -\Delta f + \frac{\partial f}{\partial S} \Delta S\]Using the obtained results so far, we have
\[\Delta \Pi = \left( -\frac{\partial f}{\partial t} - \frac{1}{2} \frac{\partial^2 f}{\partial S^2} \sigma^2 S^2 \right)\Delta t\]The above equation, does not involve \(\Delta z\), so it must be risk-less during the time \(\Delta t\). If it earned more than return, it will be a risk-less profit by borrowing money and buying the portfolio. If this portfolio earns less than r, shorting such portfolio results in a risk-less profit.
\[\Delta \Pi = r \Pi \Delta t\] \[\left( -\frac{\partial f}{\partial t} - \frac{1}{2} \frac{\partial^2 f}{\partial S^2} \sigma^2 S^2 \right)\Delta t = r \left( -f + \frac{\partial f}{\partial S} S \right) \Delta t\] \[\boxed{\frac{\partial f}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 f}{\partial S^2} +r S\frac{\partial f}{\partial S} = r f }\]The boundary condition for a European option is
- Call option at \(t=T\), \(f=\max(S-X,0)\)
- Put option at \(t=T\), \(f = \max(X-S,T)\)
Solving Black-Scholes Equation
We first take the following change of variables
\[\tilde S = \log S, \quad \tilde t = T-t\]As a result
\[\frac{\partial f}{\partial S} = \frac{1}{S} \frac{\partial f}{\partial \tilde S} , \quad \frac{\partial^2 f}{\partial S^2} = \frac{-1}{S^2} \frac{\partial f}{\partial \tilde S} + \frac{1}{S^2} \frac{\partial^2 f}{\partial \tilde S^2}, \quad \frac{\partial f}{\partial t} = -\frac{\partial f}{\partial t}\]w and the B-S equation becomes
\[- \frac{\partial f}{\partial \tilde t} + \frac{1}{2}\sigma^2 S^2 \left( \frac{-1}{S^2} \frac{\partial f}{\partial \tilde S} + \frac{1}{S^2} \frac{\partial^2 f}{\partial \tilde S^2} \right) +r S\left( \frac{1}{S} \frac{\partial f}{\partial \tilde S} \right) = r f\] \[- \frac{\partial f}{\partial \tilde t} + \frac{1}{2}\sigma^2 \frac{\partial^2 f}{\partial \tilde S^2} + \left( r- \frac{\sigma^2}{2}\right) \frac{\partial f}{\partial \tilde S} = r f\]Next, taking out the risk-free movement in the price \(\tilde f = e^{-r\tilde t}f\), we find that
\[\frac{\partial \tilde f}{\partial \tilde t} = \frac{1}{2}\sigma^2 \frac{\partial^2 \tilde f}{\partial \tilde S^2} + \left( r- \frac{\sigma^2}{2}\right) \frac{\partial \tilde f}{\partial \tilde S}\]The first derivative can also be taken out using method of lines, i.e., defining a new variable \(x =\tilde S + (r-\sigma^2/2)\tilde t\), we find that
\[\frac{\partial \tilde f}{\partial \tilde t} = \frac{\sigma^2}{2} \frac{\partial^2 \tilde f}{\partial x^2}\]where \(\tilde f = e^{-r\tilde t} f\), and \(x = \log S + (r-\sigma^2/2)\tilde t\). The initial condition then becoms that at \(\tilde t = 0\)
- Call option \(\tilde f(x,0)=\max(e^x-X,0)\)
- Put option \(\tilde f(x,0)=\max(X-e^x,0)\)
The Green’s function for the heats equation solution is
\[\frac{\partial u}{\partial t} = D \frac{\partial^2 u}{\partial x^2} \to G(t,t',x,x') = \frac{1}{\sqrt{4\pi D |t-t'|}} e^{-\frac{(x-x')^2}{4D|t-t'|}}\]As a result the solution to the above equation becomes
\[\tilde f (x,t) = \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^{\infty} e^{-\frac{(x-x')^2}{2\sigma^2 t}} \max(e^{x'}-X,0)dx'\] \[\tilde f (x,t) = \frac{1}{\sqrt{2\pi \sigma^2}} \left[ \int_{-\infty}^{\log X} e^{-\frac{(x-x')^2}{2\sigma^2 t}} (X-e^{x'})dx' + \int_{\log X}^{\infty} e^{-\frac{(x-x')^2}{2\sigma^2 t}} (e^{x'}-X)dx'\right]\]Put-Call Parity (American Option)
So far, what we have discussed was about European options. But what happens in American options? Let’s start with Put-Call parity and what it looks like for American options. Consider the following portfolios
- One stock \(S_0\) and a put option \(P\) at strike price \(X\)
- A call option \(C\) with strike price \(X\), and cash \(X\) invested at a risk free rate \(r\)
Imagine that we exercise at time \(t<T\). The payoff of the first portfolio is
\[\left[\max(X-S_t,0) + S_t\right] e^{r(T-t)} = \max(X,S_t) e^{r(T-t)}\]where we imagined that the cash received at time \(t\), is reinvested at the risk-free rate \(r\). The payoff of the second portfolio is
\[\left[ \max(S_t-X,0) + Xe^{rt} \right] e^{r(T-t)} = \left[ \max(S_t,X) + X(e^{rt}-1) \right] e^{r(T-t)} = \max(S_t,X)e^{r(T-t)} + X(e^{rT} - e^{r(T-t)})\]As a result we have
\[S_0 + P \leq C + X\]Similarly, imagine the following portfolios
- One stock \(S_0\) and a put option \(P\) at strike price \(X\)
- A call option \(C\) at strike price \(X\) and and \(Xe^{-rT}\) invested at a risk free rate \(r\)
Again, imagine that we exercise at time \(t\), again the first portfolio payoff is
\[\left[\max(X-S_t,0) + S_t\right] e^{r(T-t)} = \max(X,S_t) e^{r(T-t)}\]The second portfolio can only be traded at \(t=T\), since otherwise the money will not be enough. Therefore the payoff of the second portfolio becomes
\[\max(S_T-X,0) + X = \max(S_T,X)\]As a result, the payoff of the first portfolio is larger, or
\[C + Xe^{-rT} \leq S_0 + P\]In summary, we have
\[\boxed{C+ Xe^{-rT} \leq S_0+P \leq C+ X}\]