Goals and The Drift That Directs Your Life's Random Walk
Life can often feel like a random walk, a journey where every step is influenced by countless variables, many beyond our control. In this context, imagine each step as a day, and each direction as a decision that either takes us in positive (+1) or negative direction (-1).
When we don’t have a clear goal or purpose, our life is like a random walk with equal probabilities. Some days we make progress (+1), while on others we face setbacks (-1). Each day our steps will be
\[\text{step} = \begin{cases} +1, & p=0.5 \\ -1, & p=-0.5 \end{cases}\]Over time, after \(n\) days, the average progress is zero - meaning we stay roughly where we started - and the range of places where we might end up (the standard deviation) is quite large (proportional to \(\sqrt{n}\)). It’s unpredictable and can feel like we’re drifting aimlessly.
\[\mathbb{E}[\text{distance}] = \mathbb{E}[\text{step}_1 + \text{step}_2 + … + \text{step}_n] = n \mathbb{E}[step] = n (-1 \times 0.5 + 1 \times 0.5) = 0\] \[Var[\text{distance}] = Var[\text{step}_1 + \text{step}_2 + … + \text{step}_n] = n Var[step] = n \cdot 1 =n\]where we used the fact that
\[Var[step] = \mathbb{E}[step^2] - (\mathbb{E}[step])^2 = 1\]However, when we do have a goal, it introduces a drift, a subtle push for our walk in one direction. This goal doesn’t remove the randomness or unpredictability of life; there will still be steps forward and backward. But the drift gently nudges us towards making progress \(+1\) more often than experiencing setbacks \(-1\). It’s like a compass guiding us through the randomness. We call this a drift \(d\), that pushes us more toward one direction. So the steps each day are
\[\text{step} = \begin{cases} +1, & p=0.5+d/2 \\ -1, & p=-0.5 - d/2 \end{cases}\]Now let’s see what happens, after \(n\) days. This time the progress is not zero, in fact after \(n\) days,
\[\mathbb{E}[\text{distance}] = \mathbb{E}[\text{step}_1 + \text{step}_2 + … + \text{step}_n] = n \mathbb{E}[step] = n (-1 \times (0.5-d/2) + 1 \times (0.5+d/2)) = n\cdot d\]which means we are not at zero anymore, and in fact with that slight drift, now we are and \(n\cdot d\). It’s interesting to see that the randomness, or the standard deviation of where we are also decreases,
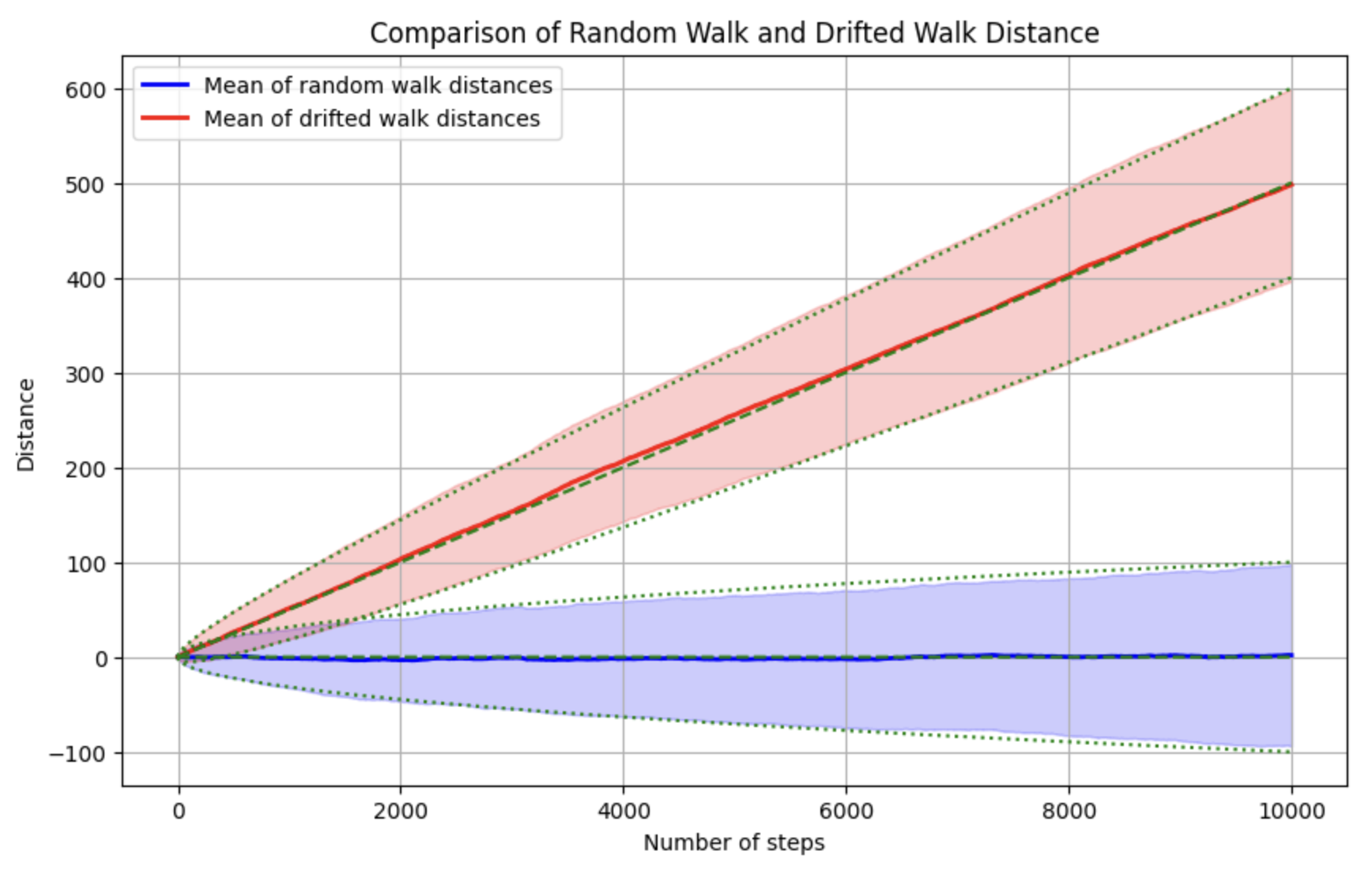
\[Var[\text{distance}] = Var[\text{step}_1 + \text{step}_2 + … + \text{step}_n] = n Var[step] = n \cdot (1-d^2)\] \[Var[step] = \mathbb{E}[step^2] - (\mathbb{E}[step])^2 = 1 - d^2\]Let’s simulate this to see it in action. We create a simulation of both a random walk example, and a drifted random walk, with setting the drift value only to ! meaning that you take a positive direction action with probability of only \(p=0.55\) (a bit more than average)!
import numpy as np
import matplotlib.pyplot as plt
# Number of steps
n = 10000
# Number of random walks
num_walks = 500
# The drift term, which makes positive steps more likely
drift = 0.05
distances_random = np.zeros((num_walks, n))
distances_drifted = np.zeros((num_walks, n))
# Perform the random walks
for i in range(num_walks):
steps_random = np.random.choice([-1, 1], size=n)
steps_drifted = np.random.choice([-1, 1], size=n, p=[0.5-drift/2, 0.5+drift/2])
distances_random[i, :] = np.cumsum(steps_random)
distances_drifted[i, :] = np.cumsum(steps_drifted)
# Calculate the mean and standard deviations of the distances at each step
mean_distances_random = np.mean(distances_random, axis=0)
mean_distances_drifted = np.mean(distances_drifted, axis=0)
mean_distances_random_theory = np.zeros(n)
mean_distances_drifted_theory = drift*np.arange(n)
std_distances_random = np.std(distances_random, axis=0)
std_distances_drifted = np.std(distances_drifted, axis=0)
# Create an array representing sqrt(n) for comparison
sqrt_n = np.sqrt(np.arange(n))
sqrt_n_drift = np.sqrt(np.arange(n)*(1 - (drift)**2))
# Plot the mean and standard deviation of the distances and sqrt(n) for comparison
plt.figure(figsize=(10, 6))
plt.plot(mean_distances_random, label='Mean of random walk distances', color='blue', lw=2)
plt.plot(mean_distances_drifted, label='Mean of drifted walk distances', color='red',lw=2)
plt.plot(mean_distances_random_theory, '--', color='green')
plt.plot(mean_distances_drifted_theory, '--', color='green')
plt.fill_between(range(n), mean_distances_random - std_distances_random, mean_distances_random + std_distances_random, color='blue', alpha=0.2)
plt.fill_between(range(n), mean_distances_drifted - std_distances_drifted, mean_distances_drifted + std_distances_drifted, color='red', alpha=0.2)
plt.plot(mean_distances_random_theory + sqrt_n, linestyle=':', color='green')
plt.plot(mean_distances_random_theory - sqrt_n, linestyle=':', color='green')
plt.plot(mean_distances_drifted_theory + sqrt_n_drift, linestyle=':', color='green')
plt.plot(mean_distances_drifted_theory - sqrt_n_drift, linestyle=':', color='green')
plt.grid()
plt.legend()
plt.xlabel('Number of steps')
plt.ylabel('Distance')
plt.title('Comparison of Random Walk and Drifted Walk Distance with sqrt(n)')
plt.show()The blue curve shows a person doing random walk, always around \(0\) with a standard deviation of \(\sqrt{n}\). The more they have lived, the more probability of being somewhere further out from \(0\) on the positive or negative side! however, when taking small actions (drift) toward a goal daily, after \(n\) days, linearly proportional to the number of days, \(n\), they are distanced from \(0\), and further more the standard deviation of their place has been reduced by \(\sqrt{n(1-d^2)}\). So take small actions daily toward a goal, as they matter a lot over a long run.