These is a review of Bayesian Machine Learning. It’s based on HSE’s course on this topic.

Maximum Likelihood Estimation (MLE)

The ML estimate for \(\theta\) is the value under which the data are most likely, i.e.

Example: We know that a fair coin has \(p(\text{head}) = p(\text{tail}) = 1/2\). Now imagine you have a coin and you don’t know if it is fair or not. You decide to throw the coin \(m\) times, where you observe \(m_H\) times head, and \(m_T\) times tail, where \(m_H + m_T = m\). Now you ask given this observation, what is the probability of \(p(\text{head}), p(\text{tail})\) for this coin? We know that if \(p(\text{head}) =\theta\), then the likelihood of such observation is

Now, we are interested to find a \(\hat \theta_{ML}\) such that the above probability is maximized. Instead of the probability, we maximize its logarithm which will be easier. We have

finding the \(\text{argmax}_\theta\) for the above equation we have

Maximum a posteriori (MAP) estimation

We learned that in MLE estimation we find \(\theta\) to maximize the likelihood function \(p(y\mid \theta)\). Now, in MAP, we find \(\theta\) such that the posterior \(p(\theta\mid y)\) is maximized, i.e.,

Since the denominator does not depend on \(\theta\), we have

The last term, \(\log p(\theta)\) is known as our prior belief.

Example: Again, imagine the same coin flip problem. Imagine we take the prior to be a beta distribution as

where \(A\) is a constant to make \(\int p(\theta)\text{d}\theta=1\). Now finding the solution to the MAP estimator, we find that

The point of \(\alpha, \beta\) coming from the prior in the above equation will be a regularizer. Imagine, we only throw the coin only once, then the ML gives \(\hat{\theta}_{ML}=1\), however, \(\hat{\theta}_{MAP} = \alpha/(\alpha+\beta)\).

Point estimation and probabilistic linear regression

Imagine we are given $m$ datapoints, \((x_1,y_1), \cdots, (x_m,y_m)\), where \(x_i\)’s are independent variables and \(y_i\)’s are dependent. Assuming a linear relationship as

where \(\epsilon \sim \mathcal{N}(0,\sigma^2)\). Assuming the independence between the \(y_i\)’s, we can write

Finding the maximum of log-likelihood, we obtain

which is the equivalent to ordinary least squares.

Now, trying the MAP estimate, we first need to assume a prior for the \(\theta\) variables. As an initial estimate we assume \(\theta \sim \mathcal{N}(0, \nu^2\mathbf{I})\). Finding the MAP solution we find that

which is the same as ML solution with a regularization term.

Conjugate priors

We often would like to find the full posterior, \(p(\theta\mid y)\). If we know the full posterior distribution, then we can do posterior predictive distribution as

The second part is because \(y_{m+1}\) and \(y\) are conditionally independent. If we would like to find the full posterior, then

The bottom part is just a normalizer. So we need to choose the prior, \(p(\theta)\), such that with the likelihood distribution, \(p(y\mid \theta)\), we are able to track the distribution. Selecting prior in such a way that the \(p(y\mid \theta)p(\theta)\) becomes tractable is known as a selection of conjugate priors for \(p(y\mid \theta)\).

Exponential families and conjugate priors

The family of distribution \(\mathcal{F}\) is called exponential family if every member of \(\mathcal{F}\) has the form

where $f(\cdot), g(\cdot), \phi(\cdot),u(\cdot)$ are some functions. For example, an exponential distribution is an exponential family distribution:

or a beta distribution:

Normal distribution is also an exponential family.

If the \(p(y_i\mid \theta)\) is coming from an exponential family distribution, then if \(y_i\)’s are independent, the likelihood becomes

Now, we can select the prior as

where \(\eta,\nu\) are hyper-parameters.

Now you might ask, doesn’t the choice of prior doesn’t matter? Can we really pick any prior distribution? In the next part, we show that as long as you pick a prior that assigns non-zero probabilities to every possible value of $\theta$, the solution of MAP converges to the true solution $\theta^$, or more precisely, $\theta^$ corresponds to the likelihood model which is closest to the true generating distribution. The closeness of the distributions is defined using KL divergence.

KL divergence

The KL divergence between two distributions \(p\) and \(q\) is defined as

Note that \(D_{KL}(p\mid \mid q)\) is always positive since

and the equality with zero only happens when \(p=q\). Now, we want to use the KL divergence to find the distribution from the likelihood family that is closest to the true generating function

Imagine we have \(y=(y_1,\cdots, y_m)\) as a set of independent samples from an arbitrary distribution \(q(y)\). We assume a family \(\mathcal{F}\) of likelihood distributions with \(\Theta = \{ \theta: p(\cdot \mid \theta) \in \mathcal{F}\}\) the finite parameter space. Our goal is to show that if \(p(\theta=\theta^*)>0\), then \(p(\theta=\theta^*\mid y)\to1\) as the number of observation increases or \(m\to\infty\). Consider \(\theta\neq \theta^*\), then

where we used the fact that \(p(\theta^*) \neq 0\). We have

Expanding the Expected value we have

The above result is negative since we assume that \(\theta^*\) minimizes the KL divergence between \(q(\cdot)\) and \(p(\cdot\mid \theta)\). So far we have found that

since the expected value we found to be negative, and as \(m\to\infty\), the value goes to negative infinity. Plugging back into the initial equation we have

This implies that \(p(\theta\mid y)/p(\theta^*\mid y) \to 0\), which means that \(p(\theta\mid y) \to 0\). We started with the fact that \(\theta\neq\theta^*\). So if \(p(\theta\mid y)\to 0\) for \(\theta\neq\theta^*\), then \(p(\theta^*\mid y)\to 1\).

Expectation Maximization

Guassian Mixture Models:

In Gaussian Mixture model, you assume that your data is coming from a combination of Gaussian (Gaussian Mixture). There is a latent variable, \(z\), that determines which Gaussian to pick or how to combine the Gaussian models. In this latent model, we are interested to find \(\theta\) parameters of the Gaussian, such that \(p(x\mid \theta)\) is maximized. Let’s assume that the latent variable is discrete and \(z=1\) or \(2\). The probability of observing a datapoint is

Our goal as usual is to find \(\max_\theta p(X\mid \theta))\). We have

So, in summary we have found the following

So, we do the above part in two steps as follows (Expectation step)

and next (Maximization step)

E-Step:

Let’s look at the E-Step. In order to do so, let’s look at the difference between the log-likelihood and the lowerbound that we defined

So we found that

which basically means that to maximize lowerbound \(\mathcal{L}(\theta,q)\) (which minimizes the distance between the log-likelihood and the lowerbound), we need to minimize the KL-divergence on the righthandside. The KL divergence is zero when the two PDFs are the same, so

M-Step:

Now we are interested to maximize the following with respect to \(\theta\) as

Summary of Expectation-Maximization:

E-step:

which results in the fact that \(\log p(X,\theta) = \mathcal{L}(\theta,q^{k+1})\). Next for the M-step, we have

Note that this maximizes the lower bound, however it is guaranteed that \(\log p(X\mid \theta^{k+1}) \geq \mathcal{L}(\theta^{k+1},q^{k+1})\)

Convergence

We have

Gaussian Mixture Models (GMM)

In these models, we assume that the data is coming from a mixture of Gaussian distributions \(\mathcal{N}(\mu,\Sigma)\) and the latent distribution is a categorical distribution \(\phi\). This basically means that

where \(\sum_k \pi_k = 1\). Note that \(\theta = \{ \mu_1,\Sigma_1, \cdots, \mu_K,\Sigma_K\}.\) Now, let’s assume the latent variable is called \(z_i\). Using Expectation-Maximization that we discussed here, we find that

Next, in the Maximization step, we have

Taking the derivative with respect to the \(\mu_k\), we find that

Similarly, we can find that

K-Means as EM

Imagine the K-means model, where we randomly initialize \(\theta = \{\mu_1, \cdots, \mu_C\}\) points, and then we repeat the following steps until convergence

• For each point we calculate the closest centroid

• Update centroid

The above K-means model can be think of as a GMM. Imagine we fix the covariance matrix to be identity, $\Sigma_k = I$, and also we fix the weights to be \(\pi_k = 1/\#\text{of Gaussians}\). We then will have

Then, in the E-step, we pick \(q(z)\) such that they belong to the delta functions. Then are interested to find a function from the family of delta functions such that

Note that

So the above maximization problem becomes

which is the same as the first step in the K-means. Now, lets look at the M-step, using the GMM derivation that we did above, we ha

Implementing GMM in python

So in GMM we are implementing the following formulae

E-step:

M-Step:

from scipy import stats
# here we denote q(z_i=k) with a NxC matrix called gamma
# where N is the number of poitns i=1,...,N
# and C is the number of clusters
def E_step(X, pi, mu, sigma):
    """
    Performs E-step on GMM model
    Each input is numpy array:
    X: (N x d), data points
    pi: (C), mixture component weights
    mu: (C x d), mixture component means
    sigma: (C x d x d), mixture component covariance matrices

    Returns:
    gamma: (N x C), probabilities of clusters for objects

    P(z\mid x) = (p(x\mid z) p(z))/(sum_z p(x\mid z) p(z) )
    gamma  =
    """
    N = X.shape[0] # number of objects
    C = pi.shape[0] # number of clusters
    d = mu.shape[1] # dimension of each object
    gamma = np.zeros((N, C)) # distribution q(T)
    for i in range(C):
      pi_i = pi[i]
      gamma[:,i] = pi_i*stats.multivariate_normal(mu[i,:],sigma[i,:,:]).pdf(X)

    gamma = gamma/np.sum(gamma,axis=1).reshape(-1,1)

    return gamma

def M_step(X, gamma):
    """
    Performs M-step on GMM model
    Each input is numpy array:
    X: (N x d), data points
    gamma: (N x C), distribution q(T)

    Returns:
    pi: (C)
    mu: (C x d)
    sigma: (C x d x d)
    """
    N = X.shape[0] # number of objects
    C = gamma.shape[1] # number of clusters
    d = X.shape[1] # dimension of each object

    resp_weights = np.sum(gamma,axis=0)
    pi = resp_weights/(1.0*N)

    mu = np.dot(gamma.T,X)/resp_weights.reshape(-1,1)

    sigma = np.zeros((C,d,d))

    for i in range(C):
      diff = (X-mu[i])
      weighted_sum = np.dot((gamma[:,i].reshape(-1,1)*diff).T,diff)
      sigma[i,:,:] = weighted_sum/resp_weights[i]

    return pi, mu, sigma

def train_EM(X, C, rtol=1e-3, max_iter=100, restarts=10):
    '''
    Starts with random initialization *restarts* times
    Runs optimization until saturation with *rtol* reached
    or *max_iter* iterations were made.

    X: (N, d), data points
    C: int, number of clusters
    '''
    N = X.shape[0] # number of objects
    d = X.shape[1] # dimension of each object
    best_loss = -np.inf
    best_pi = None
    best_mu = None
    best_sigma = None

    for _ in range(restarts):
        try:
            pi = np.ones(C)/float(C)
            mu = np.random.randn(C,d)
            sigma = np.zeros((C,d,d))
            sigma[...] = np.identity(d)
            prev_loss = None
            for _ in range(max_iter):
              gamma = E_step(X,pi,mu,sigma)
              pi,mu,sigma = M_step(X,gamma)
              loss = compute_vlb(X,pi,mu,sigma,gamma)

              if not np.isnan(loss) and loss>best_loss:
                best_loss = loss
                best_mu = mu
                best_pi = pi
                best_sigma = sigma

              if prev_loss is not None:
                diff = np.abs(prev_loss-loss)/np.abs(prev_loss)
                if diff < rtol:
                  break
              prev_loss = loss

        except np.linalg.LinAlgError:
            print("Singular matrix: components collapsed")
            pass

    return best_loss, best_pi, best_mu, best_sigma

Benefits of GMM models: in unsupervised clustering for example, KNN methods accuracy will increase as we increase the number of groups. So you never know how many groups are better for KNN methods. In GNN on the other hand, the accuracy increases and then decreases. So increasing the number of clusters does not necessary increase the accuracy.

Dirichlet Distribution

A Dirichlet distribution is defined as

Note that \(\sum_{i=1}^K \theta_i = 1\) and \(\theta_i>0\). The expected value and variance can be found as

Note that the Dirichlet distribution is conjugate to the multinomial distribution as

So if prior has a Dirichlet distribution, and likelihood is a multinomial, then the posetrior will also be a Dirichlet distribution.

Latent Dirichelet Model

Imagine the following model for the distribution of words in a document

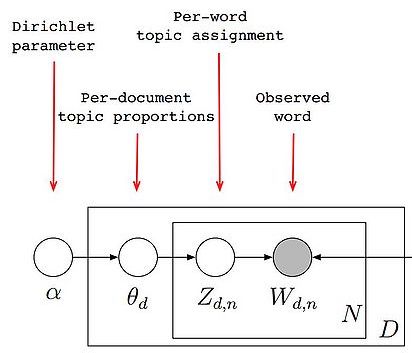
In latent Dirichelet model, we have

where \(p(\theta_d)\sim \text{Dir}(\alpha)\), and \(p(z_{dn}\mid \theta_d) = \theta_{dz_{dn}}\), and \(p(w_{dn}\mid z_{dn}) = \Phi_{z_{dn},w_{dn}}\), where \(\sum \Phi_{z_{dn},w_{dn}} =1\). In order to calculate the E-step, we first need to find the log-likelihood, where we have

In the E-step, we want to

So in summary, we have

Now, let’s take the E-step for \(q(Z)\), we have

so in summary

and in the M-step we would like to maximize the following

given that \(\sum_w \phi_{tw} = 1\) and also \(\phi_{tw}\geq 0\). We use lagrangian to maximize the above equation, we have

Now we take the derivative to maximize the above equation, we find

Knowing that \(\sum_w \phi_{tw} = 1\), we can find that

Monte-Carlo Method

Estimating expected values using sampling

Now the question is how to sample from a probability distribution \(p(x)\)? In the following we will discuss this. Note that we assume that generating a random number with uniform distribution from in \([0,1]\) is given, i.e., we can easily sample form \(\mathcal{U}(0,1)\).

Sampling from 1-D distribution

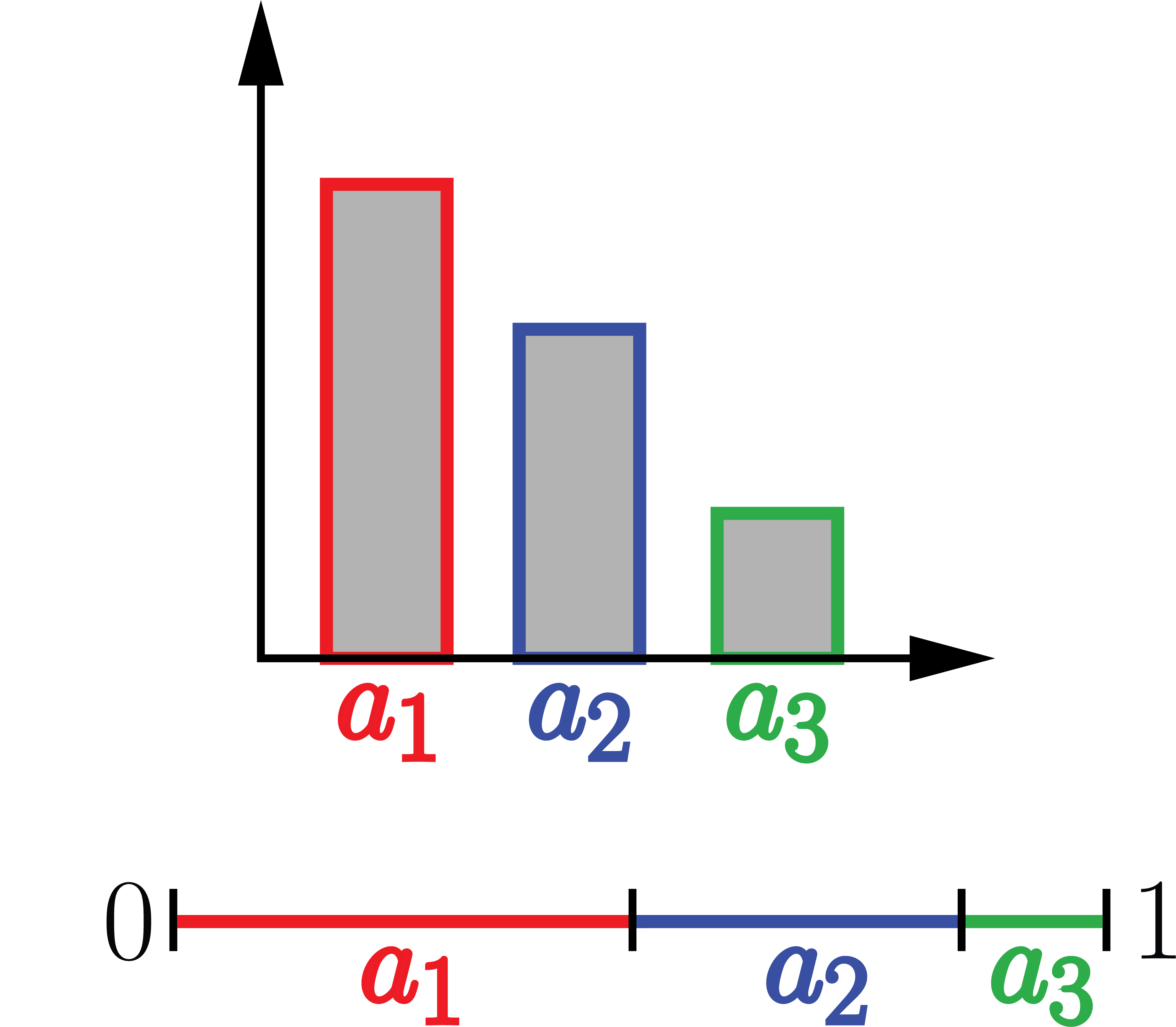
Consider a distribution over discrete set such as \(p(a_i) = p_i\) for \(i=1,\cdots,n\). Note that \(\sum_i p_i = 1\). We can separate the \([0,1]\) distance proportional to the \(p_i\). Next, we sample a point from $[0,1]$ using the uniform distribution, we can assign it to the discrete values of \(a_i\) based on the interval that it lands into. Here is an example:

Sampling Normal distribution:

We can generate normal distribution using central limit theorem, i.e.

As the \(N\to \infty\), the \(p(x) \to \mathcal{N}(0,1)\). This has been done very efficiently, and we can use packages such as np.random.randn() to generate these numbers. Now imagine that we are interested in 1d sampling from a continuous distribution such as \(p(x)\) shown below

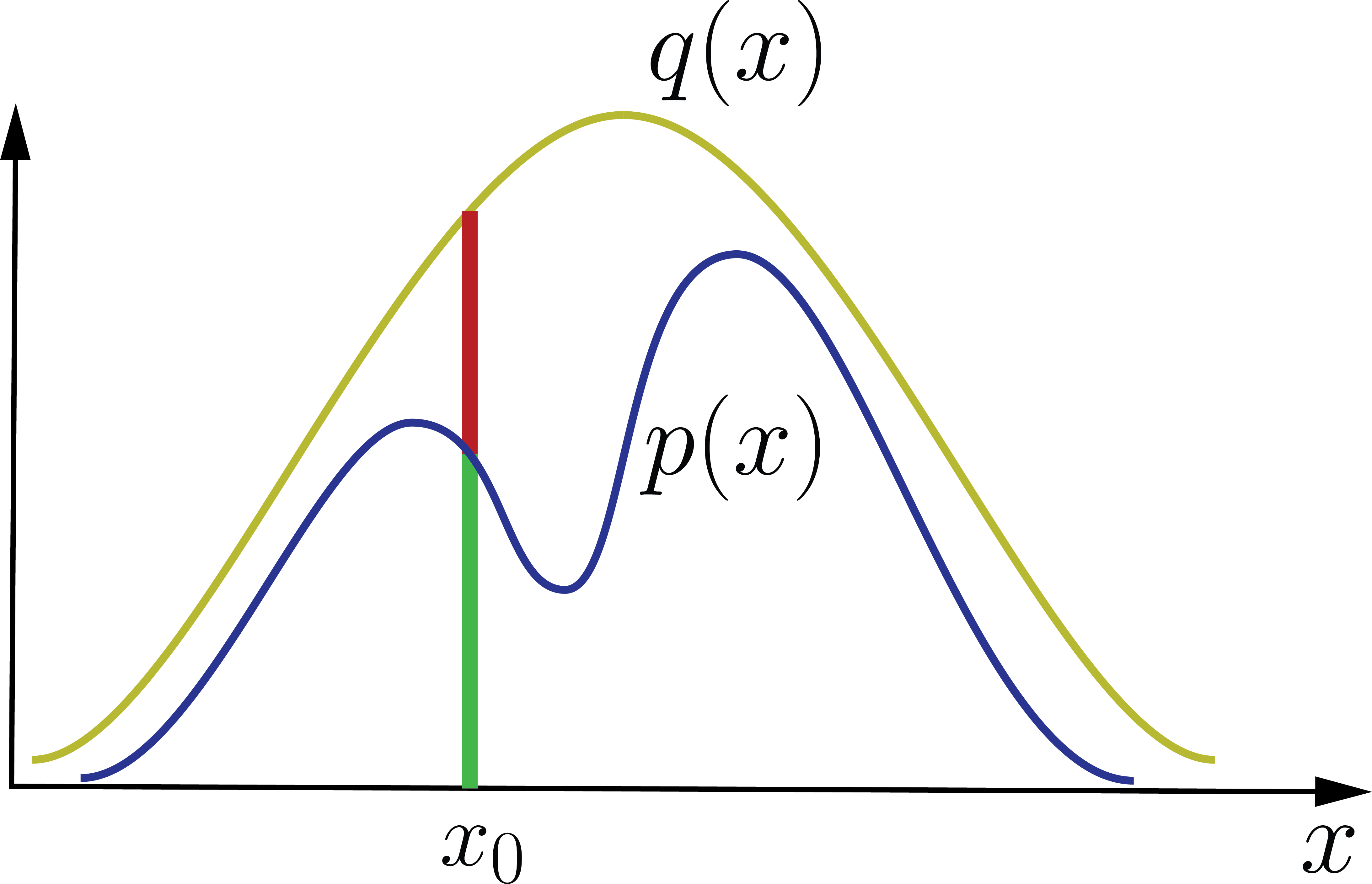
One way to sample from \(p(x)\) in the above is to first bound the pdf by some normal distribution $q(x)$. Next, we generate a random point, say \(x_0\). We then accept this point with probability \(\alpha= p(x)/q(x)\) and reject it with \(1-\alpha\). This way, we create samples from the \(p(x)\).

Markov-Chains

There are two methods that we will introduce here (Metropolis-Hasting and Gibbs sampling) that depend on Markov-Chain. A few introductory remarks on Markov-process is helpful before we talk about them.

Let \(X_t\) denote the value of a random variable at time $t$. The state space is the space of all possible values for $X$ values. The random variable is called a Markov process if the transition probabilities betwen different values in the state space only depend on the current’s value of the random variable, i.e.,

A Markov-Chain referes to a sequence of random variables \((X_0, \cdots,X_n)\) generated by a markov process. Transition probability (or the transition kernel) gives us the probability of transitioning between the states ina single step, i.e.,

Using the transition kernel, if we are at state \(s_i\) we can define a row vector for the state space probabilities, i.e., \(\pi_i(t) = p(X_t = s_i)\). The evolution of this state space probabilities can be obtained using the kernel as

As a result, we can find that \(\pi(t) = \pi(0) \mathbf{P}^k\). A distribution of states $\mathbf{\pi}^*$ is called stationary if \(\mathbf{\pi}^* = \mathbf{\pi}^*\mathbf{P}\). A sufficient condition for a unique stationary distribution is that the detailed balance condition holds

If the above condition holds then we have

Metropolis-Hasting Algorithm

So our goal is to generate a sample with PDF \(p(x)\). In Metropolis-Hasting the basic idea is to create a Markov-Process to generate new data points where \(p(x)\) is its stationary distribution. If \(p(x)\) is stationary distribution, then using following the Markov process for a long time we will generate data-points that have the distribution of \(p(x)\). But how can we create a Markov-Process where \(p(x)\) is its stationary distribution? We can use the idea of rejecting points. We start with any Markov-process \(Q\) (as long as we have a non-zero probability of going over all the data points), we then start from a data-point \(x_0\) (or state) and find our new data-point \(x_1\) (the new state). Now we have an option of accepting this new state or rejecting it. We select this acceptance/rejection probability such that our \(p(x)\) becomes the stationary distribution of our Markov process.

So as long as our acceptance probability follows the above equality, we are doing well. Assume that the above proportionality is \(\rho\). If \(\rho\leq 1\), we can have \(A(x_0\to x_1) = \rho, A(x_1\to x_0) = 1\). On the other hand, if \(\rho>1\), we can assign \(A(x_0\to x_1) = 1, A(x_1\to x_0) = 1/\rho\). So basically, we can assign the following acceptance probability

Or we can summarize it as